刘硕的技术查阅手册

Python 全栈开发学习笔记

0%

插入排序和希尔排序

发表于 更新于 分类于
插入排序同选择排序和冒泡排序一样，原理很简单，但效率较低。希尔排序是在插入排序的基础上进行的优化，提高了效率。

插入排序（Insertion sort）

插入排序，就是将数据一个一个比较，找到自己合适的位置，插入进去。

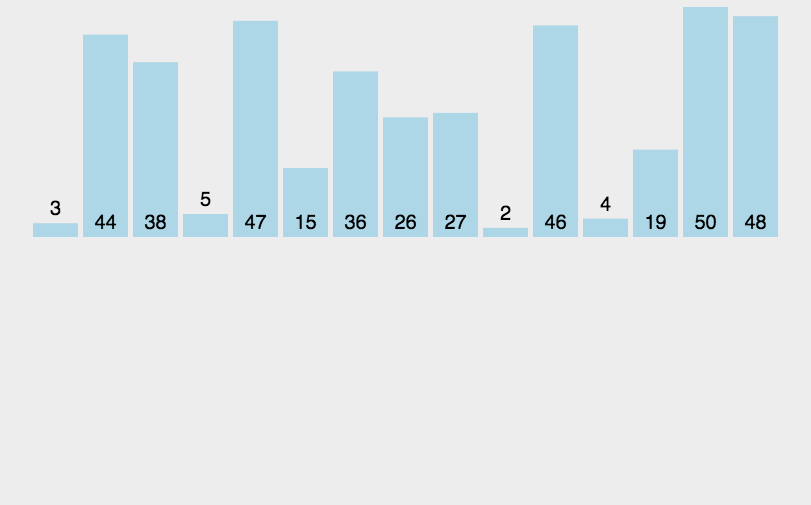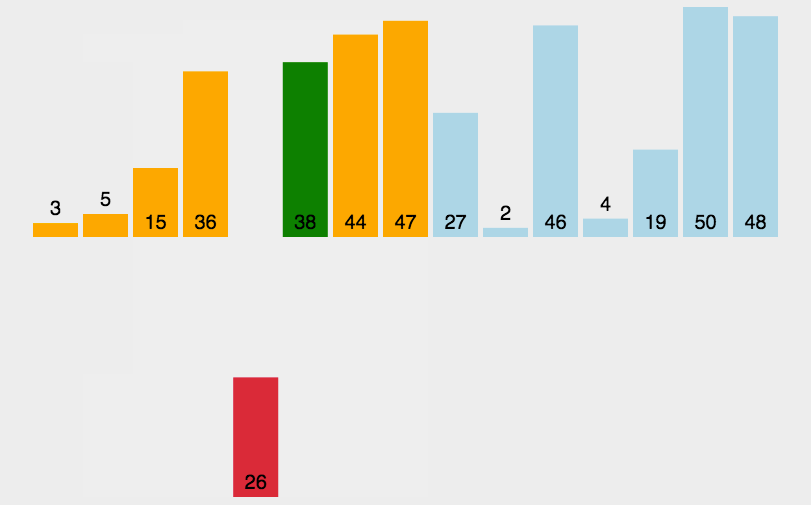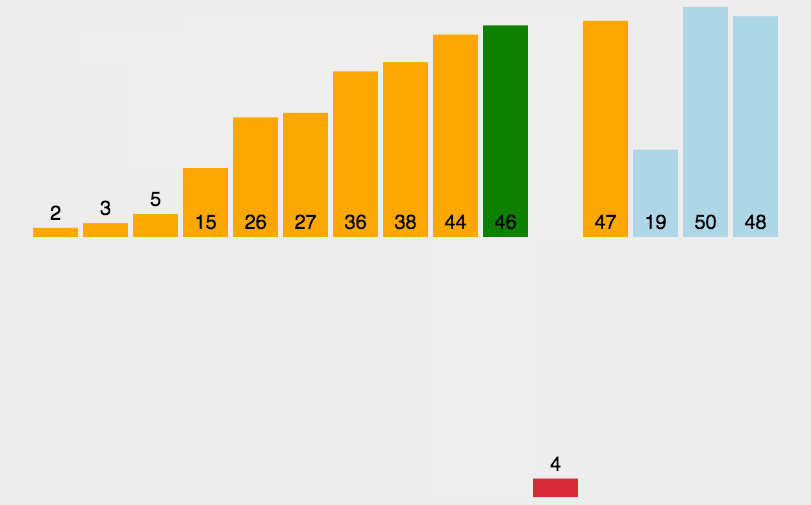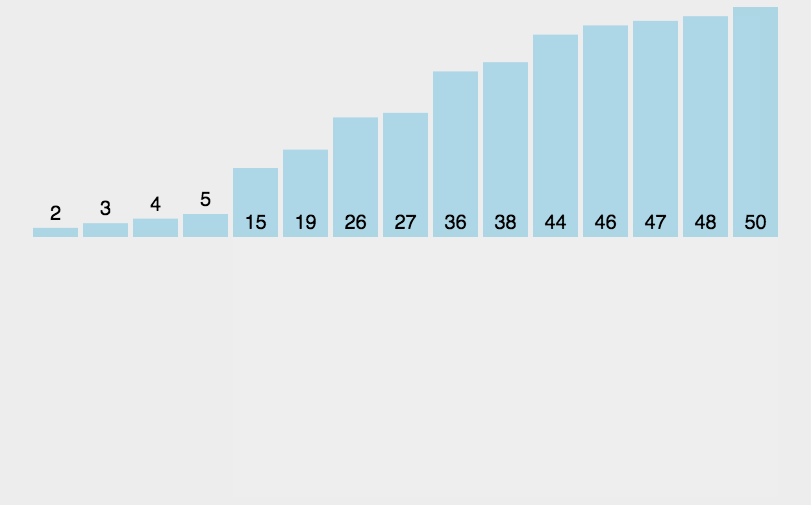
思路：

  • 需要将原始序列分成两部分：有序部分，无序部分

  • 将无序部分中的元素逐一插入到有序部分中

  • 初始情况下，有序部分为乱序序列的第一个元素，无序部分为乱序序列的其余 n - 1 个元素

  • 比如，对于乱序序列：[3, 8, 5, 7, 6]

    1
    2
    3
    4
    5
    [3, , , , 8, 5, 7, 6]    # 3就是初始的有序部分，8，5，7，6就是初始的无序部分
    [3, 8, , , , 5, 7, 6]
    [3, 5, 8, , , , 7, 6]
    [3, 5, 7, 8, , , , 6]
    [3, 5, 6, 7, 8, , , ,]

  • 定义一个变量 i，i 表示的是有序部分元素的个数 & 无序部分第一个元素下标。

首先，我们来考虑第一步。最开始有序部分是第一个元素。一个元素一定是有序的。我们用第二个元素同第一个元素比较，如果第二个元素比第一个元素小，则两者进行交换，否则不需要进行操作：

1
2
3
4
5
6
7
alist = [31, 8, 5, 7, 6]
i = 1    # i就是有序部分元素的个数&有序部分最后一个下标+1&无序部分第一个元素下标
# alist[i - 1]：有序部分最后一个元素下标
# alist[i]：无序部分第一个元素下标
if alist[i] < alist[i - 1]:
    alist[i], alist[i - 1] = alist[i - 1], alist[i]
print(alist)    # [8, 31, 5, 7, 6]

接下来，我们让代码继续执行。当前两个元素的顺序排好之后，我们就要将第三个元素放到合适的位置。如何找呢？从后往前，挨个比较，直到之前的元素比他小位置，或者走到最前面：

1
2
3
4
5
6
7
8
9
10
11
# 承接上步，alist = [8, 31, 5, 7, 6]
i = 2
while i >= 1:    # i在这里的作用是记录有序元素的个数
    if alist[i] < alist[i - 1]:    # i是有序部分最后一个下标+1&无序部分第一个元素下标
        # 循环第一次执行[8,5,31,   7,6]
        # 循环继续执行  [5,8,31,   7,6]
        alist[i], alist[i - 1] = alist[i - 1], alist[i]
        i -= 1
    else:
        break
print(alist)

我们发现，只需要把 i 的值递增上去，上面的代码还可以继续使用，比如 i 增加到 3：

1
2
3
4
5
6
7
8
i = 3
while i >= 1:
    if alist[i] < alist[i - 1]:
        alist[i], alist[i - 1] = alist[i - 1], alist[i]
        i -= 1
    else:
        break
print(alist)    # [5, 7, 8, 31, 6]

我们当然不可能自己这么增加 i 的值。相反，我们可以使用 for 循环获取新的 i 值。同时，可以把代码封装成函数形式。插入排序的完整代码为：

1
2
3
4
5
6
7
8
9
10
11
12
alist = [3, 8, 5, 7, 6]
def insertion_sort(alist):
    # 处理变量i，需要让i进行自己递增
    for i in range(1, len(alist)):
        while i >= 1:
            if alist[i] < alist[i - 1]:
                alist[i], alist[i - 1] = alist[i - 1], alist[i]
                i -= 1
            else:
                break
    return alist
print(insertion_sort(alist))    # [3, 5, 6, 7, 8]

希尔排序（Shell sort）

希尔排序是插入排序的一种，也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量（gap）”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高。

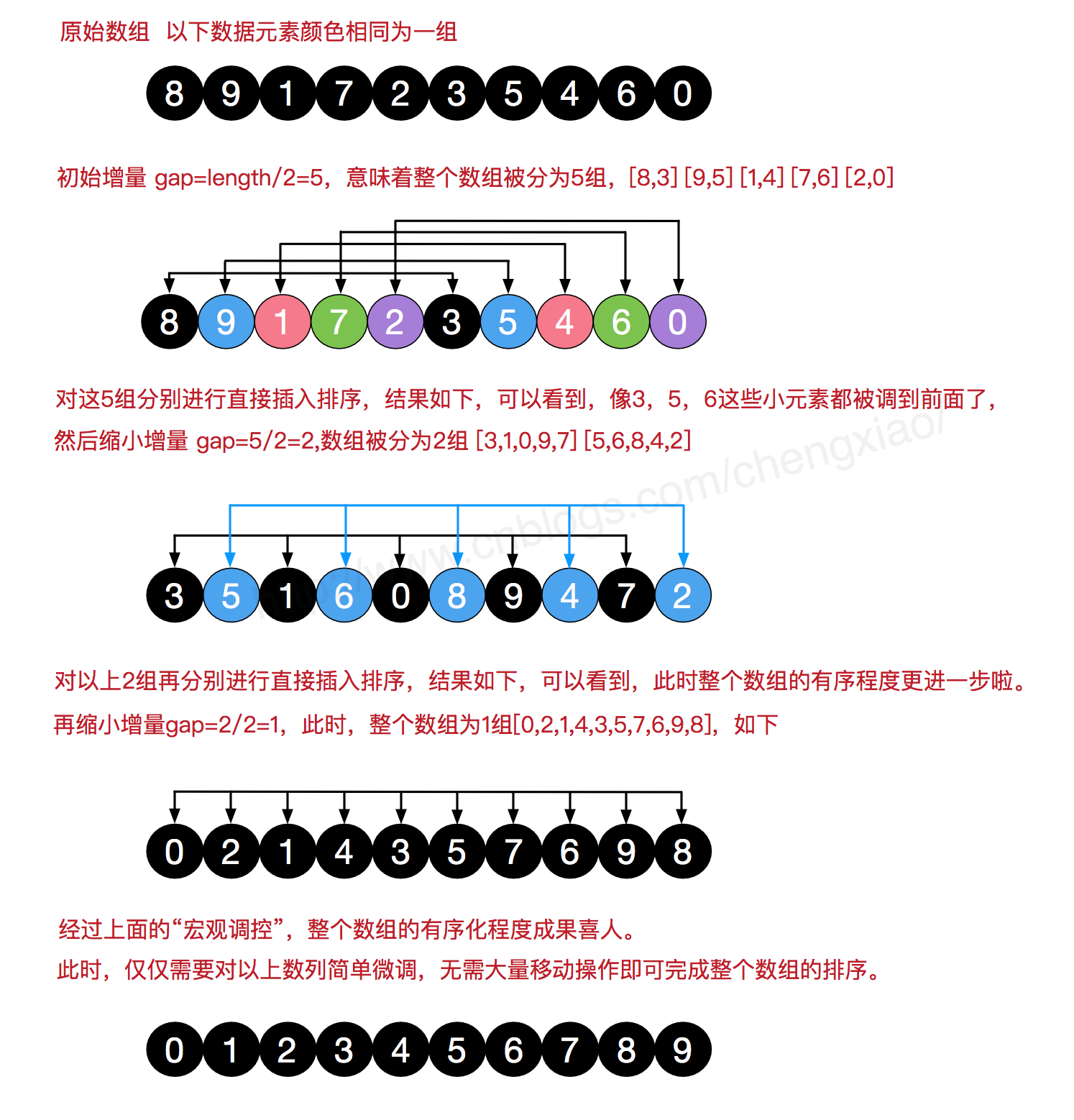
关键变量：增量 gap

  • gap：初始值为 len(alist) // 2
    1. 表示分组的组数
    2. 每一组数据之间的间隔

插入排序就是增量为1的希尔排序。

首先，我们在插入排序中引入增量的概念。增量初始值设置为列表长度的一半。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
alist = [3, 8, 5, 7, 6, 9, 2, 1, 4]    # 测试数据要多一些，这样能看出隐藏的问题来
def shell_sort(alist):
    gap = len(alist) // 2    # 初始增量
    # 将插入排序中所有增量1替换成gap
    # 由增量为1变成了增量为gap了
    for i in range(gap, len(alist)):
        while i >= gap:
            if alist[i] < alist[i - gap]:
                alist[i], alist[i - gap] = alist[i - gap], alist[i]
                i -= gap
            else:
                break
    return alist
print(shell_sort(alist))

然后，引入循环逐步将 gap 减半，直到为 1，即实现希尔排序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
alist = [3, 8, 5, 7, 6, 9, 2, 1, 4]
def shell_sort(alist):
    gap = len(alist) // 2    # 初始增量
    while gap >= 1:
        for i in range(gap, len(alist)):
            while i >= gap:
                if alist[i] < alist[i - gap]:
                    alist[i], alist[i - gap] = alist[i - gap], alist[i]
                    i -= gap
                else:
                    break
        gap //= 2    # 缩减增量
    return alist
print(shell_sort(alist))