栈

本节将介绍一个重要的编程概念—调用栈（call stack）。调用栈不仅对编程来说很重要，使用递归时也必须理解这个概念。

栈是一种后进先出的数据结构，只有弹出和两种操作：

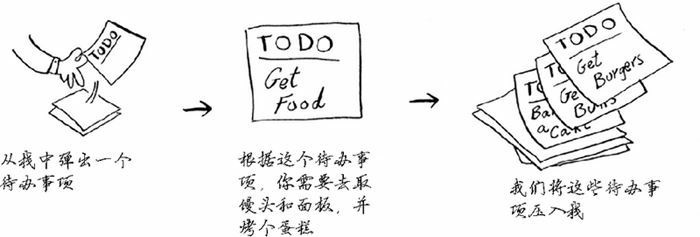
调用栈

计算机在内部使用被称作调用栈的栈。

来看下面的函数调用：

def greek(name):
    print('hello, ' + name + '!')
    greek2(name)
    print('getting ready to say bye...')
    bye()


def greek2(name):
    print('how are you, ' + name + '?')


def bye():
    print('ok bye!')


greek('maggie')

为简便起见，下面的讨论先不把 print 看作函数了。

当我们调用 greet('maggie') 函数时，计算机将首先为该函数调用分配一块内存。我们来使用这些内存。变量name 被设置为 maggle，这需要存储到内存

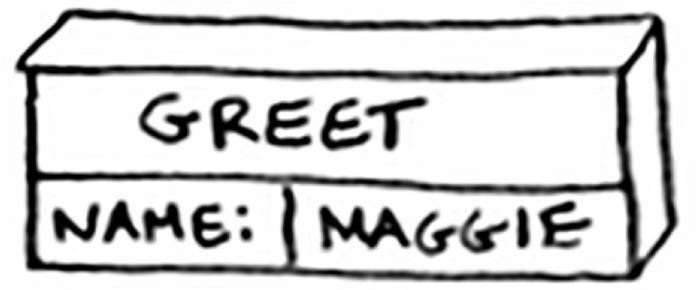
函数 greet 从上向下执行，只要函数没有执行完，内存就不会被释放。最开始，是打印出一串内容，hello, maggie!。随后，调用 greek2 函数，参数 name 还是 maggie。需要注意的是，此时 greek 函数尚未执行完毕，所以内存不会释放，而因为调用了 greek2，还要给它一块内存空间，就放在 greek 空间的上面。这种层叠的空间存储结构，就是调用栈。

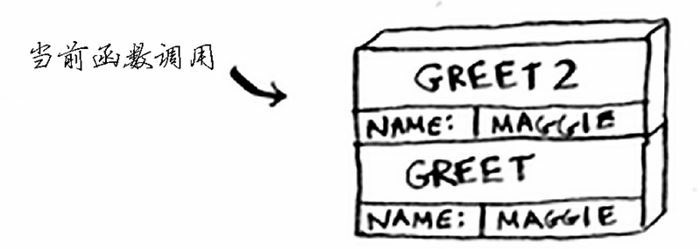
此时，greek 暂时被搁置，活跃的是最上方的 greek2 函数。它从上往下执行，打印出 how are you, maggie? 后，运行完毕，释放内存空间。栈顶端的 greet2 占用的内存块被弹出。

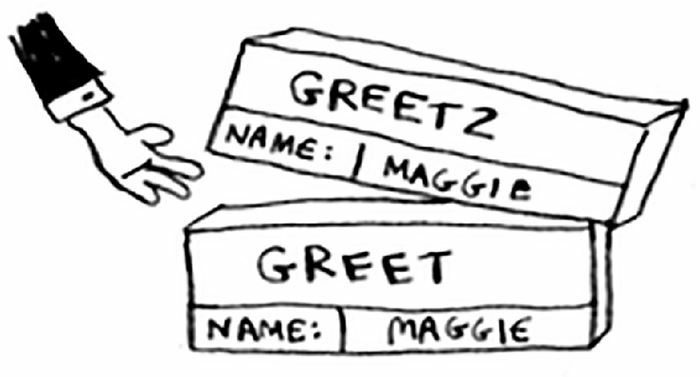
此时，活跃的函数又是 greek 了。调用 greek2 的步骤已经执行完毕，接着往下走，打印出 getting ready to say bye... 之后，又调用了 bye 函数。同样道理，bye 函数的内存块被压倒栈的顶端。

bye 运行，打印出 ok bye! 后，释放内存空间，从栈顶段弹出。

greet 的最后一行代码也执行完，它也从栈中弹出。这个栈用于存储多个函数的变量，称为调用栈。

递归调用栈

递归函数也使用调用栈！来看看递归函数 factorial 的调用栈。factorial(5) 写作 5!，其定义如下：5! = 5 * 4 * 3 * 2 * 1。同理，factorial(3) 为 3 * 2 * 1。下面是计算阶乘的递归函数：

def fact(n: int):
    if n == 1:
        return n
    else:
        return n * fact(n - 1)


print(fact(5))    # 120
print(fact(3))    # 6

下面来详细分析调用 fact(3) 时调用栈是如何变化的。别忘了，栈顶的方框指出了当前执行到了什么地方。

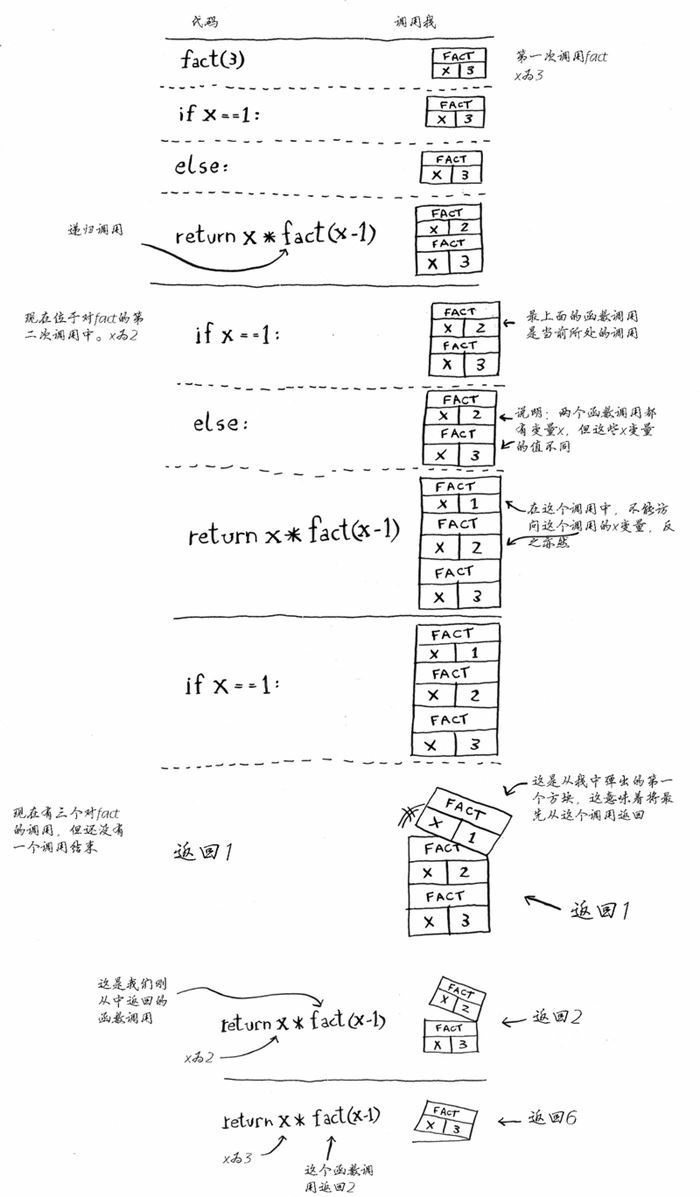
注意，每个 fact 调用都有自己的 x 变量。在一个函数调用中不能访问其他函数的 x 变量。

递归调用栈包含未完成的函数调用，每个函数调用都包含还未检查完的盒子。使用栈很方便，因为你无需自己跟踪盒子堆——栈替你这样做了。

使用栈虽然很方便，但是也要付出代价：存储详尽的信息可能占用大量的内存。每个函数调用都要占用一定的内存，如果栈很高，就意味着计算杋存储了大量函数调用的信息。在这种情况下，你有两种选择：

• 重新编写代码，转而使用循环。
• 使用尾递归。这是一个高级递归主题，不在本书的讨论范围内。另外，并非所有的语言都支持尾递归。