刘硕的技术查阅手册

Python 全栈开发学习笔记

0%

双蛋问题的 Python 递归解决

发表于 更新于 分类于
手里有 2 个鸡蛋，另外有 100 层楼。有一未知的临界楼层，鸡蛋从临界楼层以下扔下去，一定不会碎；从临界楼层以上丢下去，一定会碎。没有摔碎的鸡蛋可以反复使用，碎了的鸡蛋就不能再往下扔了。问，在最糟糕的情况下，至少需要多少次能够找到临界楼层？

今天看了 李永乐老师关于双蛋问题的讲解视频，受用很大。本着好记性不如烂笔头的精神，把这个问题记录在此。

据传某大厂有这样一个面试题：手里有 2 个鸡蛋，另外有 100 层楼。有一未知的临界楼层，鸡蛋从临界楼层以下扔下去，一定不会碎；从临界楼层以上丢下去，一定会碎。没有摔碎的鸡蛋可以反复使用，碎了的鸡蛋就不能再往下扔了。问，在最糟糕的情况下，至少需要多少次能够找到临界楼层？

吐槽一句，这个鸡蛋可能比较特殊，因为普通鸡蛋别说 100 层楼，从桌子上掉下去基本就碎了。不过问题本身是很有价值的，我们可以把鸡蛋改成玻璃球之类的，低楼层摔不碎，高楼层受不了就成了。

另外，要想读懂本文，恐怕需要一点递归和算法基础，否则不一定能看懂。这不是因为我水平高，写的东西高深莫测。而是因为我的水平太低，道行太浅，目前还没办法做到深入浅出，十分抱歉。

好了，闲话不多扯，来谈谈解决问题的思路。

二分查找解决无限多鸡蛋的情况

直接看问题，似乎没什么思路。我们不妨稍微简化一下问题。比如，如果我们有无数多个鸡蛋，最坏的情况下至少需要几个鸡蛋能找到临界楼层？

这就很简单了，使用二分法即可。先从 50 层试，如果鸡蛋碎了，说明临界楼层在下面，就去 25 层再试；如果鸡蛋没碎，说明临界楼层在上面，到 75 层去试。以此类推，每次排除一半的可能，很快就能找到答案。

二分法需要的次数的公式是 $log_2(100)$ 向下取整再加 1，计算结果应该是 7。

递归法解决双蛋问题

不过二分查找似乎并没有对我们解决问题有什么特别好的启发，我们只好另辟蹊径。我们可不可以通过 分而治之 的思想来解决这个问题呢？

首先，基线条件很好确定：

  1. 在有 2 个鸡蛋的情况下，如果只有一层楼，只需要试一次；如果有两层楼，只需要试两次；如果没有楼，那就干脆不用试了（看似是废话，但是是很重要的边界条件）。
  2. 如果只有 1 个鸡蛋，只能老老实实从下往上尝试，也就是在最坏的情况下，有几层楼就要试几次。

接下来，我们就要思考递归条件了。如何能将问题简化。

令在有 2 个鸡蛋时，最坏的情况下，N 层楼所需要尝试的最少次数为 $T_N$。

假设总共有 N 层楼，我们在第 K 层楼进行一次尝试。那么此时，就会分成两种情况：

  1. 鸡蛋在 K 层碎掉了，也就说明临界楼层在 K 层以下。但是此时，我们只剩下 1 个鸡蛋，最坏的情况下还要检测 $K - 1$ 次才能找到临界楼层
  2. 鸡蛋在 K 层没有碎，临界楼层在 K 层以上。此时我们还是有 2 个鸡蛋，还剩下 $N-K$ 层楼需要检测，那么最坏的情况下，还需要检测 $T_{N-K}$ 次。很显然 $N-K$ 要比 N 少，我们顺利实现对问题的简化。

最坏的情况显然是 $K - 1$ 和 $T_{N-K}$ 两个数的最大的那一个再加上 1，因为我们先试了一次。这个最大的数，就是 $T_N$。

不过这里面有一个 K 是不能确定的。为了找到合适的 K，我们需要把 K 从 1 到 N 的情况全部计算出来，找到使得 $T_N$ 最小的情况即可。

用代码来解决这个问题就是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def two_egg(n: int) -> int:
    """
    双蛋问题的递归求解
    :param n: 楼层数
    :return: 最坏情况下，找到临界楼层所需最少尝试次数
    """
    if n == 0:    # 没有楼就不需要试
        return 0
    elif n == 1:   # 有一层楼，试一次
        return 1
    result_list = []
    for k in range(1, n + 1):    # 在每一层都试一下
        result_list.append(max(k - 1, two_egg(n - k)) + 1)    # 把每一层的情况都记录下来
    return min(result_list)    # 最好的结果就是我们想要的


# 用 1 到 11 的数字测试，不用 100 是因为电脑性能不够，测到 11 是因为 10 和 11 的结果不同
for f in range(1, 12):
    print(f'{f} -------> {two_egg(f)}')

上面的代码用到了递归。随着递归层数的增加，会占用很多资源，计算时间也会特别长。可以通过记录低楼层的结果，优化上面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def two_egg_opt(n: int, result_dict: dict) -> int:
    if n in result_dict:
        return result_dict[n]
    else:
        result_list = []
        for k in range(1, n + 1):  # 在每一层都试一下
            result_list.append(max(k - 1, two_egg_opt(n - k, result_dict)) + 1)  # 把每一层的情况都记录下来
        result_dict[n] = min(result_list)  # 最好的结果就是我们想要的
        return min(result_list)

# 从前计算的结果记录在result_dict中，下次使用可以直接拿，极大减少了递归层数
result_dict = {0: 0, 1: 1}
for i in range(1, 101):
    result_dict[i] = two_egg_opt(i, result_dict)
print(result_dict)

优化前的代码用我的小电脑根本无法求出 100 层楼的双蛋问题的解。而使用这个优化后的代码，1 到 100 层楼双蛋问题的解几乎立刻就出来了。

递归法解决普遍双蛋问题

用二分查找，可以解决鸡蛋数目不限的情况，递归查找可以解决只有 2 个鸡蛋的情况。现在，我们把问题进一步扩展：如果我们有 M 个鸡蛋，N 层楼，在最坏的情况下，至少需要测试多少次能够找到临界楼层？

基线条件根上面的差不多一样：

  1. 不管有多少个鸡蛋，如果只有一层楼，只需要试一次；如果没有楼，那就干脆不用试了。
  2. 如果只有 1 个鸡蛋，只能老老实实从下往上尝试，也就是在最坏的情况下，有几层楼就要试几次。

递归条件其实也很类似，只是因为鸡蛋数目的引入，会稍微复杂一丁丁点点。

令在有 M 个鸡蛋时，最坏的情况下，N 层楼所需要尝试的最少次数为 $T_{M,\space N}$。

依旧假设总共有 N 层楼，我们在第 K 层楼进行一次尝试。那么此时，还是会分成两种情况：

  1. 鸡蛋在 K 层碎掉了，也就说明临界楼层在 K 层以下。但是此时，我们只剩下 $M-1$ 个鸡蛋，最坏的情况下还要检测 $T_{M-1,\space K - 1}$ 次才能找到临界楼层
  2. 鸡蛋在 K 层没有碎，临界楼层在 K 层以上。此时我们还是有 M 个鸡蛋，还剩下 $N-K$ 层楼需要检测，那么最坏的情况下，还需要检测 $T_{M,\space N-K}$ 次

上面的两种情况，要么简化了鸡蛋数量，要么简化了楼层数量，最终都可以通过递归来找到答案。最终的结果需要是 $T_{M-1,\space K - 1}$ 和 $T_{M,\space N-K}$ 这两个数中最大的那一个加上 1，因为我们最开始的时候在 K 层测试了一下。

同样地，我们需要遍历测试当 K 为 1 到 N 时的各种情况，取其中所需步骤最少的，就是我们要的结果。

用代码表示就是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def two_egg_general(m: int, n: int) -> int:
    """
    普遍双蛋问题的解决
    :param m: 鸡蛋数量
    :param n: 楼层总层数
    :return: 最糟糕的情况下，找到临界楼层所需最少尝试数目
    """
    if n == 0:    # 如果没有楼，不需要试
        return 0
    elif n == 1:    # 只有 1 层楼，试一次就足够
        return 1
    if m == 1:    # 只有 1 个蛋，有几层楼就要使几次
        return n
    result_list = []
    for k in range(1, n + 1):
        result_list.append(max(two_egg_general(m - 1, k - 1), two_egg_general(m, n - k)) + 1)
    return min(result_list)


for i in range(1, 12):
    for j in range(1, 12):
        print(f'({i}, {j}) --> {two_egg_general(i, j)}', end=' | ')
    print()

测试结果如下：

附上双蛋问题的参照表，都是吻合的。只不过我是以楼层数为横轴，鸡蛋数为纵轴了而已。

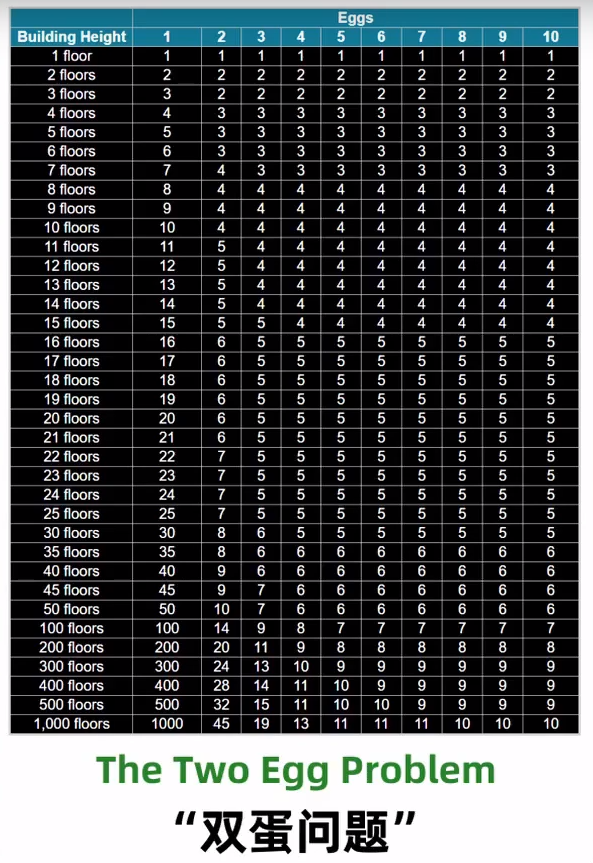
同样地，也可以对这个代码进行优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def two_egg_gen_opt(m: int, n: int, result_dict: dict) -> int:
    """
    普遍双蛋问题递归解决的优化
    :param m: 鸡蛋数量
    :param n: 楼层总层数
    :param result_dict: 储存结果的字典
    :return: 最糟糕的情况下，找到临界楼层所需最少尝试数目
    """
    if (m, n) in result_dict:
        return result_dict[(m, n)]
    if n == 0:    # 如果没有楼，不需要试
        result_dict[(m, n)] = 0
        return 0
    elif n == 1:    # 只有 1 层楼，试一次就足够
        result_dict[(m, n)] = 1
        return 1
    if m == 1:    # 只有 1 个蛋，有几层楼就要使几次
        result_dict[(m, n)] = n
        return n
    result_list = []
    for k in range(1, n + 1):
        result_list.append(max(two_egg_gen_opt(m - 1, k - 1, result_dict), two_egg_gen_opt(m, n - k, result_dict)) + 1)
    result_dict[(m, n)] = min(result_list)
    return min(result_list)


result_dict = {}
for i in range(1, 20):
    for j in range(1, 1002):
        print(f'({i}, {j}) --> {two_egg_gen_opt(i, j, result_dict)}', end=' | ')
    print()